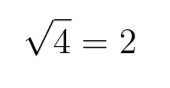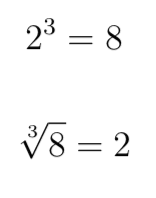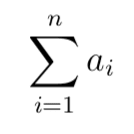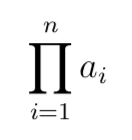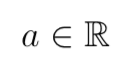Vous ne pouvez pas éviter la notation mathématique lors de la lecture des descriptions des méthodes d'apprentissage automatique.

Souvent, il suffit d'un terme ou d'un fragment de notation dans une équation pour complètement faire dérailler votre compréhension de l'ensemble de la procédure. Cela peut être extrêmement frustrant, en particulier pour les débutants en machine learning issus du monde du développement.

A lire également : Qu'est-ce qu'un formulaire ABA ?

Vous pouvez faire de grands progrès si vous connaissez quelques domaines de base de la notation mathématique et quelques astuces pour décrire les méthodes d'apprentissage automatique dans les articles et les livres.

Dans ce tutoriel, vous découvrirez les bases de la notation mathématique que vous pouvez rencontrer lors de la lecture de descriptions de techniques d'apprentissage automatique.

A découvrir également : Quelle est la meilleure façon d'apprendre le piano ?

Après avoir terminé ce tutoriel, vous saurez :

• Notation pour l'arithmétique, y compris les variations de multiplication, les exposants, les racines et les logarithmes.
• Notation pour les séquences et les ensembles, y compris l'indexation, la somme et l'appartenance à un ensemble.
• 5 techniques vous pouvez utiliser pour obtenir de l'aide si vous avez des difficultés avec la notation mathématique.

Lancez votre projet avec mon nouveau livre Linear Algebra for Machine Learning, qui comprend des tutoriels étape par étape et les fichiers de code source Python pour tous les exemples.

Allons-y.

• Mise à jour mai/2018  : ajout d'images pour certaines notations afin de clarifier les explications.

Les bases de la notation mathématique pour l'apprentissage automatique Photo de Christian Collins, certains droits réservés.

Aperçu du didacticiel

Ce tutoriel est divisé en 7 parties, à savoir :

1. La frustration liée à la notation mathématique
2. Notation arithmétique
3. Alphabet grec
4. Notation de séquence
5. Notation d'ensemble
6. Autre notation
7. Obtenir plus d'aide

Y a-t-il d'autres domaines de la notation mathématique de base nécessaires à l'apprentissage automatique qui, selon vous, m'ont échappé ? Faites-moi savoir dans le commentaires ci-dessous.

Besoin d'aide concernant l'algèbre linéaire pour l'apprentissage automatique ?

Prenez maintenant mon cours intensif gratuit de 7 jours par e-mail (avec un exemple de code).

Cliquez pour vous inscrire et obtenez également une version PDF Ebook gratuite du cours.

Téléchargez votre mini-cours GRATUIT

La frustration liée à la notation mathématique

Vous rencontrerez une notation mathématique lorsque vous lirez des algorithmes d'apprentissage automatique.

Par exemple, la notation peut être utilisée pour :

• Décrivez un algorithme.
• Décrire la préparation des données.
• Décrivez les résultats.
• Décrivez un harnais d'essai.
• Décrivez les implications.

Ces descriptions peuvent figurer dans des articles de recherche, des manuels, des articles de blog, etc.

Les termes sont souvent bien définis, mais il existe également des normes de notation mathématique que vous ne connaissez peut-être pas.

Il suffit d'un terme ou d'une équation que vous ne comprenez pas et votre compréhension de l'ensemble de la méthode sera perdue. J'ai J'ai moi-même souffert de ce problème plusieurs fois, et c'est incroyablement frustrant !

Dans ce tutoriel, nous allons passer en revue quelques notations mathématiques de base qui vous aideront à lire les descriptions des méthodes d'apprentissage automatique.

Notation arithmétique

Dans cette section, nous allons passer en revue quelques notations moins évidentes pour l'arithmétique de base ainsi que quelques concepts que vous avez peut-être oubliés depuis l'école.

Arithmétique simple

La notation pour l'arithmétique de base est telle que vous l'écrirez. Par exemple :

• Ajout : 1 1 = 2
• Soustraction : 2 — 1 = 1
• Multiplication : 2 x 2 = 4
• Division : 2/2 = 1

La plupart des opérations mathématiques ont une opération sœur qui effectue l'opération inverse ; par exemple, la soustraction est l'inverse de l'addition et la division est l'inverse de la multiplication.

Algèbre

Nous voulons souvent décrire les opérations de manière abstraite pour les séparer de données spécifiques ou d'implémentations spécifiques.

Pour cela raison pour laquelle nous voyons une utilisation intensive de l'algèbre : c'est-à-dire des lettres majuscules et/ou minuscules ou des mots pour représenter des termes ou des concepts en notation mathématique. Il est également courant d'utiliser des lettres de l'alphabet grec.

Chaque sous-domaine des mathématiques peut comporter des lettres réservées : c'est-à-dire des termes ou des lettres qui ont toujours la même signification. Néanmoins, les termes algébriques doivent être définis comme faisant partie de la description et s'ils ne le sont pas, il se peut que ce soit une mauvaise description, ce n'est pas de votre faute.

Notation de multiplication

La multiplication est une notation courante et possède quelques aiguilles courtes.

Souvent, un petit « x » ou un astérisque « * » est utilisé pour représenter la multiplication :

c = A X B c = A * B Vous pouvez voir une notation par points utilisée, par exemple :

c = a. b Ce qui est le même que :

c = A * B Vous pouvez également ne voir aucune opération et aucune séparation d'espaces blancs entre les termes précédemment définis, par exemple :

c = ab Ce qui, encore une fois, c'est pareil.

Exposants et racines carrées

Un exponent est un nombre élevé à une puissance.

La notation est écrite sous la forme du nombre d'origine, ou de la base, avec un deuxième nombre, ou l'exposant, affiché en exposant ; par exemple :

2^3 Ce qui serait calculé comme 2 multiplié par lui-même 3 fois, ou cubing :

2 x 2 x 2 = 8 Un nombre élevé à la puissance 2 à est dit être son carré.

2 ^ 2 = 2 x 2 = 4 Le carré d'un nombre peut être inversé en calculant la racine carrée. Ceci est affiché en utilisant la notation d'un nombre et avec une coche au-dessus, j'utiliserai la fonction « sqrt () » ici pour plus de simplicité.

sqrt (4) = 2

Ici, nous connaissons le résultat et l'exposant et nous souhaitons en trouver la base.

En fait, l'opération racine peut être utilisée pour inverser n'importe quel exposant, il se trouve que la racine carrée par défaut suppose un exposant de 2, représenté par un indice 2 devant la graduation de la racine carrée.

Par exemple, nous pouvons inverser le cubage d'un nombre en prenant la racine cubique (notez que le 3 n'est pas une multiplication ici, il s'agit d'une notation avant la coche du signe racine) :

2^3 = 8 3 sqrt (8) = 2

Logarithmes et e

Lorsque nous élevons 10 à un exposant entier, nous appelons souvent cela un ordre de grandeur.

10 ^ 2 = 10 x 10 ou 100 Une autre façon d'inverser cette opération consiste à calculer le logarithme du résultat 100 en supposant une base de 10 ; en notation, il est écrit log10 ().

log10 (100) = 2 Ici, nous connaissons le résultat et la base et souhaitons trouver l'exposant.

Cela nous permet de monter et de descendre très facilement des ordres de grandeur. Prenant le logarithme en supposant que la base de 2 est également couramment utilisée, étant donné l'utilisation de l'arithmétique binaire utilisée dans les ordinateurs. Par exemple :

2^6 = 64 log2 (64) = 6 Un autre logarithme populaire est de prendre la base naturelle appelée e. Le e est réservé et est un nombre spécial ou une constante appelée nombre d'Euler (prononcé « oy-ler «) qui fait référence à une valeur avec une précision pratiquement infinie.

e = 2,71828... L'élever à un pouvoir, c'est appelée fonction exponentielle naturelle :

e^2 = 7,38905... Il peut être inversé en utilisant le logarithme naturel, qui est désigné par ln () :

ln (7,38905...) = 2 Sans entrer dans les détails, l'exposant naturel et le logarithme naturel s'avèrent utiles dans l'ensemble des mathématiques pour décrire de façon abstraite la croissance continue de certains systèmes, par exemple des systèmes qui croissent de façon exponentielle tels que l'intérêt composé.

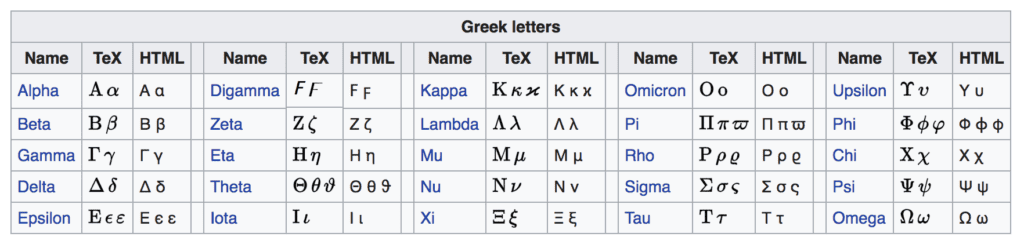
Alphabet grec

Les lettres grecques sont utilisées dans toute la notation mathématique pour les variables, les constantes, les fonctions, etc.

Par exemple, dans les statistiques, nous parlons de la moyenne utilisant la lettre grecque minuscule mu et de l'écart type en minuscule grecque sigma. En régression linéaire, nous parlons des coefficients en tant que lettre bêta minuscule. Et ainsi de suite.

Il est utile de connaître toutes les lettres grecques majuscules et minuscules et de savoir comment les prononcer.

Quand j'étais étudiant aux cycles supérieurs, j'ai imprimé l'alphabet grec et je l'ai collé sur mon écran d'ordinateur pour pouvoir Mémorisez-le. Une astuce utile !

Vous trouverez ci-dessous l'alphabet grec complet.

Alphabet grec, tiré de Wikipédia

La page Wikipédia intitulée « Lettres grecques utilisées en mathématiques, sciences et ingénierie » est également un guide utile car elle répertorie les utilisations courantes de chaque lettre grecque dans différents sous-domaines des mathématiques et des sciences.

Notation de séquence

La notation du Machine Learning décrit souvent une opération sur une séquence.

Une séquence peut être un tableau de données ou une liste de termes.

Indexation

La notation des éléments d'indexation de la séquence est une clé pour lire la notation des éléments d'indexation dans la séquence.

Souvent, la notation spécifiera le début et la fin de la séquence, par exemple 1 à n, où n sera l'étendue ou la longueur de la séquence.

Les éléments de la séquence sont indexés par une variable telle que i, j, k en tant qu'indice. C'est comme la notation de tableau.

Par exemple, a_i est le i^e élément de la séquence un.

Si la séquence est bidimensionnelle, deux indices peuvent être utilisés, par exemple :

b_ {i, j} est le i, j ^e élément de la séquence b.

Opérations de séquence

Les opérations mathématiques peuvent être effectuées sur une séquence.

Deux opérations sont effectuées sur des séquences si souvent qu'elles ont leur propre raccourci : la somme et la multiplication.

Sommation des séquences

La somme d'une séquence est désignée par la lettre grecque sigma majuscule. Il est spécifié avec la variable et le début de la somme de la séquence sous le sigma (par exemple i = 1) et l'indice de fin de la somme au-dessus du sigma (par exemple n).

Sigma i = 1, n a_i

Il s'agit de la somme de la séquence a commençant à l'élément 1 à l'élément n.

Multiplication séquence

La multiplication sur une séquence est désignée par la lettre grecque majuscule pi. Il est spécifié de la même manière que la somme de la séquence avec le début et la fin de l'opération en dessous et au-dessus de la lettre respectivement.

Pi i = 1, n a_i

Il s'agit du produit de la séquence a partant de l'élément 1 jusqu'à l'élément n.

Notation d'ensemble

Un ensemble est un ensemble d'objets uniques.

Nous pouvons voir une notation d'ensemble utilisée lors de la définition de termes en apprentissage automatique.

Ensemble de chiffres

Un ensemble courant que vous pouvez voir est un ensemble de nombres, tel qu'un terme défini comme faisant partie de l'ensemble des entiers ou de l'ensemble des nombres réels.

Certains ensembles de chiffres courants que vous pouvez voir incluent :

• Ensemble de nombres naturels : N
• Ensemble de tous les entiers : Z
• Ensemble de tous les nombres réels : R

Il existe d'autres séries ; voir Séries spéciales sur Wikipedia.

Nous parlons souvent de valeurs réelles ou de nombres réels lors de la définition de termes plutôt que de valeurs à virgule flottante, qui sont des créations vraiment discrètes pour les opérations sur ordinateurs.

Adhésion définie

Il est courant de voir l'appartenance à un ensemble dans les définitions des termes.

L'appartenance à un ensemble est désignée par un symbole qui ressemble à un « E » majuscule.

à E R

Ce qui signifie que a est défini comme étant un membre de l'ensemble R ou de l'ensemble des nombres réels.

Il existe également une multitude d'opérations d'ensemble. Les deux opérations d'ensemble courantes sont les suivantes :

• Union ou agrégation : A U B
• Intersection ou chevauchement : A ^ B

Pour en savoir plus sur les décors, consultez Wikipédia.

Autre notation

Il existe d'autres notations que vous pouvez rencontrer.

J'essaie d'en exposer une partie dans cette section.

Il est courant de définir une méthode dans l'abstrait, puis de la définir à nouveau comme une implémentation spécifique avec une notation distincte.

Par exemple, si nous estimons une variable x, nous pouvons la représenter à l'aide d'une notation qui modifie le x ; par exemple :

La même notation peut avoir une signification différente dans un contexte différent, tel qu'une utilisation sur différents objets ou sous-domaines des mathématiques. Par exemple, un point de confusion courant est |x|, ce qui, selon le contexte, peut signifier :

• |x| : Le valeur absolue ou positive de x.
• |x| : La longueur du vecteur x.
• |x| : La cardinalité de l'ensemble x.

Ce tutoriel ne couvrait que les bases de la notation mathématique. Certains sous-domaines des mathématiques sont plus pertinents pour l'apprentissage automatique et devraient être examinés plus en détail. Ce sont les suivants :

• Algèbre linéaire.
• Statistiques.
• Probabilité.
• Calcul.

Et peut-être un peu d'analyse multivariée et de théorie de l'information.

Y a-t-il des domaines de notation mathématique qui, selon vous, manquent dans cet article ? Faites-le moi savoir dans les commentaires ci-dessous.

5 conseils pour obtenir de l'aide avec la notation mathématique

Cette section répertorie quelques conseils que vous pouvez utiliser lorsque vous rencontrez des difficultés avec la notation mathématique en apprentissage automatique.

Pensez à l'auteur

Les gens ont écrit le journal ou le livre que vous lisez.

Les personnes qui peuvent faire des erreurs, des omissions et même rendre les choses confuses parce qu'elles ne comprennent pas tout à fait ce qu'ils écrivent.

Relâchez légèrement les contraintes de la notation que vous lisez et pensez à l'intention de l'auteur. Qu'est-ce qu'ils essaient de faire passer ?

Peut-être pouvez-vous même contacter l'auteur par e-mail, Twitter, Facebook, LinkedIn, etc., et demander des éclaircissements. N'oubliez pas que les universitaires veulent que d'autres personnes comprennent et utilisent leur travail (principalement).

Consultez Wikipedia

Wikipédia possède des listes de notation qui peuvent aider à préciser le sens ou l'intention de la notation que vous lisez.

Je vous recommande de commencer par deux endroits :

• Liste des symboles mathématiques sur Wikipedia
• Lettres grecques utilisées en mathématiques, en sciences et en ingénierie sur Wikipédia

Croquis dans le code

Les opérations mathématiques ne sont que des fonctions sur des données.

Associez tout ce que vous lisez à un pseudocode avec des variables, des boucles for et plus encore.

Vous pouvez utiliser un langage de script au fur et à mesure, ainsi que de petits tableaux de des données contriées ou même une feuille de calcul Excel.

Au fur et à mesure que votre lecture et votre compréhension de la technique s'amélioreront, votre croquis de code de la technique aura plus de sens et, à la fin, vous aurez un mini-prototype avec lequel jouer.

Je n'ai jamais fait le point sur cette approche avant de voir un croquis académique d'un article très complexe en quelques lignes de matlab avec des données techniques. Cela m'a fait tomber les pieds parce que je croyais que le système devait être complètement codé et fonctionner avec un « vrai » jeu de données et que la seule option était d'obtenir le code et les données d'origine. Je me suis trompé. De plus, avec le recul, le gars était doué.

J'utilise maintenant cette méthode tout le temps et des techniques d'esquisse en Python.

Chercher des alternatives

Il y a une astuce que j'utilise lorsque j'essaie de comprendre une nouvelle technique.

Je trouve et lis tous les articles qui font référence à l'article que je lis avec la nouvelle technique.

La lecture d'autres universitaires, l'interprétation et la réexplication de la technique peuvent clarifie souvent mes malentendus dans la description originale.

Mais pas toujours. Parfois, cela peut brouiller les eaux et introduire des explications trompeuses ou une nouvelle notation. Mais le plus souvent, cela aide. Après avoir fait le tour de l'article original et l'avoir relu, je trouve souvent des cas où des articles ultérieurs ont effectivement commis des erreurs et des interprétations erronées de la méthode originale.

Postez une question

Il existe des endroits en ligne où les gens adorent expliquer les mathématiques aux autres. Sérieusement !

Pensez à prendre une capture d'écran de la notation avec laquelle vous avez du mal, à écrire la référence complète ou le lien vers celle-ci, et à la publier ainsi que votre zone de malentendu sur un site de questions-réponses.

Voici deux bons points de départ :

• Mathématiques Stack Exchange
• Validation croisée

Quelles sont tes astuces pour travailler avec la notation mathématique ? Faites-le moi savoir dans les commentaires ci-dessous ?

Lectures supplémentaires

Cette section fournit plus de ressources sur le si vous souhaitez aller plus loin.

• La section 0.1. Lecture de mathématiques, calcul vectoriel, algèbre linéaire et formes différentielles, 2009.
• Le langage et la grammaire des mathématiques, Timothy Gowers
• Comprendre les mathématiques, un guide, Peter Alfeld.

Résumé

Dans ce didacticiel, vous avez découvert les bases de la notation mathématique que vous pouvez rencontrer lors de la lecture de descriptions de techniques d'apprentissage automatique.

Plus précisément, vous avez appris :

• Notation pour l'arithmétique, y compris les variations de multiplication, les exposants, les racines et les logarithmes.
• Notation pour les séquences et les ensembles, y compris l'indexation, la somme et l'appartenance aux ensembles.
• 5 techniques que vous pouvez utiliser pour obtenir de l'aide si vous avez des difficultés avec la notation mathématique.

Vous avez des difficultés avec la notation mathématique ?

Est-ce que l'une des notations ou des conseils de cet article vous a aidé ? Faites-le moi savoir dans les commentaires ci-dessous.